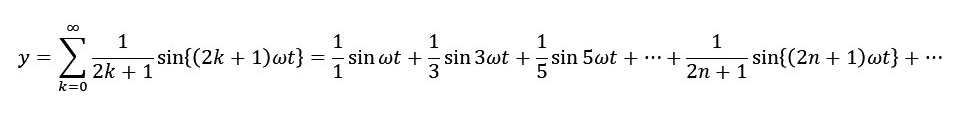人類の歴史上で賢い人間を挙げろと言われたら、私は2名の人物を推します。Faraday (ファラデー)とFourier (フーリエ)さんです。

　ファラデーさんは、電気磁気学(電磁気学)がもたらす物理現象を一つ一つ実験的に明らかにしていった人です。電磁気学は後年Maxwell方程式でまとめられたように、Maxwellさんが電磁気学の最終的な勝利者と言えなくもないですが、その基礎を造ったファラデーさんの実験力と観察力にはそれ以上に脱帽です。

　一方のフーリエさんは 、その名を取ったフーリエ級数で有名な人です。フーリエ級数曰く、「あらゆる周期関数は、三角関数の級数和で示される」です。なーんてこと思いつきます?　その発想力には脱帽です。

　カクカクした矩形波をフーリエ級数で表すと、

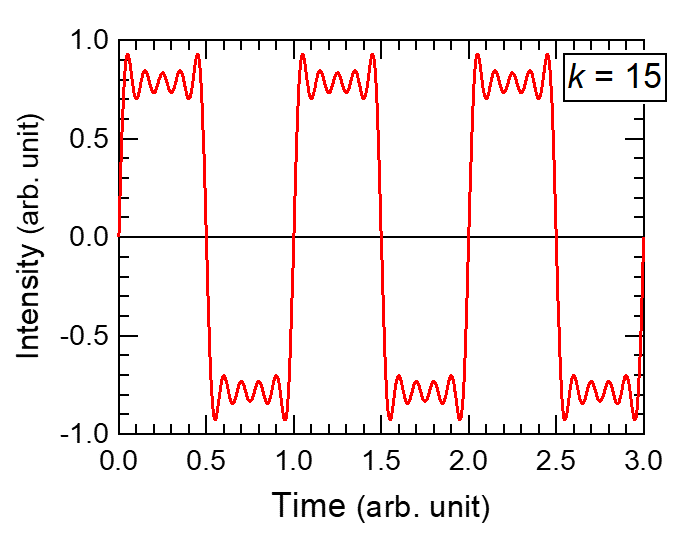
という式になります。これをグラフソフトで描いてみます。愛用のソフトはIgor Proです。∞までの和をとるのは不可能なので、k = 15までに留めると、

という形状になります。

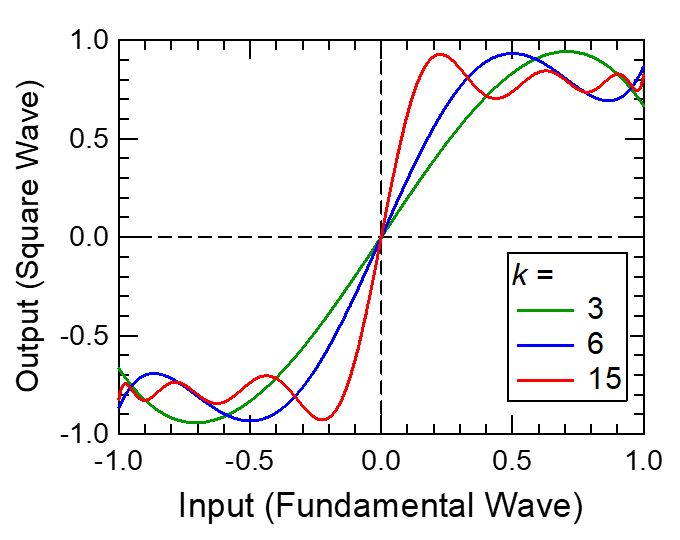
　さて、これをLissajous (リサジュー)図にして遊んでみます。fundamental wave (基本波)すなわちsin ωtをx軸に、矩形波フーリエ級数をy軸にすると、

となります。kが大きくなり真の矩形波に近づいていくほど、グラフは断崖絶壁のように立ってきます。一般にはこのようなグラフ形状は、sigmoid (シグモイド)と呼ばれています。統計学の累積分布関数もこんな形になりますが、それは理解できます。へー、リサジュー図形でもこうできるんでするね。

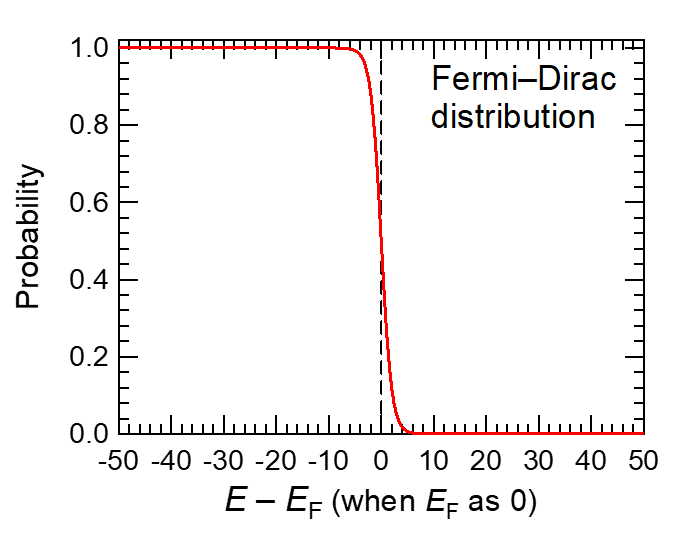
　ん、あれれー?　このグラフ、どこかで見た形だな・・・。そう、Fermi-Dirac分布関数の形状です。Fermi-Dirac分布関数 とは、

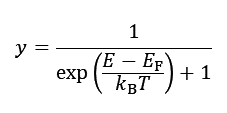
で与えられる関数で、固体中の電子のエネルギー分布を示します。グラフにすると、

です。まあー、似ていると言っても、左右が反転してるんですけどねー。

　そんな感じでちょっと考えてみます。量子力学では、電子は粒子であり、かつ波でもあります。古典物理学の範疇では、とても想像できない話です。「粒子と波動の二重性」ですね。人間も結局は電子からできていますから、我々も波動の一つの形となります。

　波動??　「私はクネクネ人ではないわよ!!」、というアナタ。この世の中の時空間自体が波動の場合、その中に生きる我々は、我々自身を波動とは感じないはずですよね。我々自身の周りにはあらゆる周波数の電磁波があります。それらを利用して、我々は情報通信をしています。電磁波は空間の歪みとも言えますが、光を除けば我々はそれを感じません。

　我々は基本波をベースとした時空間に存在しており、この矩形波のようなまとまった形を成す物は、 Fermi-Dirac分布的に言えば高エネルギー状態となる。

・・・まったく、何言ってんだか。

　でもね、研究というものは、こんなとりとめのないカオスから始まるんですよ。

　そう、Ji、 Ji、 Ji、 JiJiJi、 Ji、自由な研究!!

Views: 113